The Doppler Effect

Doleron, CC BY-SA 3.0 <https://creativecommons.org/licenses/by-sa/3.0>, via Wikimedia Commons

Even if you've never heard of the Doppler effect, you may have experienced it. When a vehicle speeds by you with its horn continuously blowing, its pitch changes from high to low. It's fairly easy to understand this without having to wade through a lot of math. Let's explain the concept using a train of bullets fired from a moving gun.

A marksman shooting at a target with a stopwatch time the bullet's journey

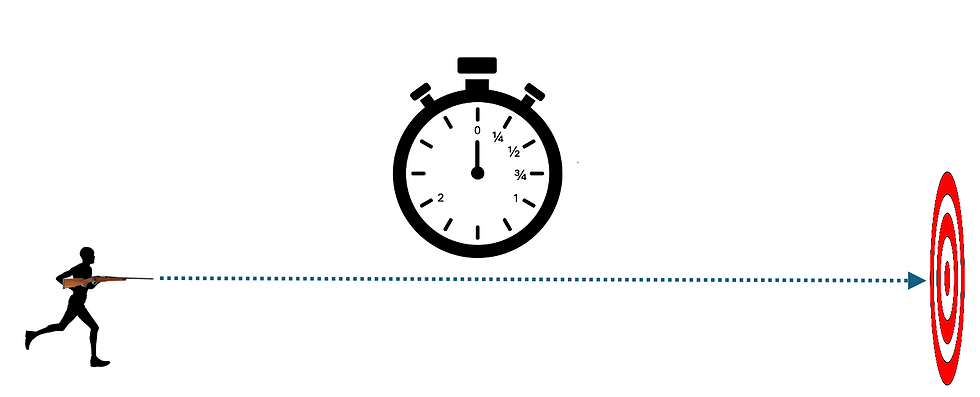
Target practice

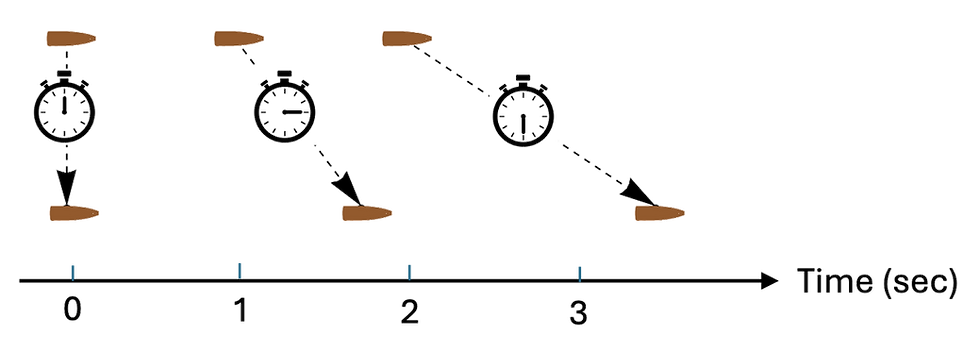
Suppose there's a marksman shooting at a target, firing at regular time intervals, for example, one shot every second. The flight time of each bullet is measured with a stop watch; let's say it takes 3/4 of a second for the bullet to get to the target. The picture below shows the timing of four successive bullets. The target is getting hit by a bullet at the same frequency as they were fired, one bullet per second.

Timing of four bullets for stationary shooter. Top row: Times when the gun is fired. Bottom row: Times when the target is hit. The stopwatches show the flight times of the bullets.

This marksman, however, is also a very fast and agile runner, and he can run and shoot accurately at the same time. Suppose he runs toward the target while shooting at 1-second intervals. Now how often will the target get hit? The same as before, more often, or less often? Let's redraw the timing picture:

Timing of bullets for shooter running toward the target

Because he's getting closer and closer to the target, each bullet has a shorter distance to travel than the previous one and therefore a shorter flight time. When he fires the fourth bullet, he has reached the target, so the bullet hits it immediately. We can see from the above picture that the target is now being hit more frequently than once per second.

Now suppose he goes into reverse and runs away from the target while still shooting once per second. (This guy is seriously agile.) Now each bullet has a longer flight time than the previous one. The target is now being hit less frequently than once per second:

Timing of bullets for shooter running away the target

These pictures show only the timing of events. Let's show what happens when we picture the space of the practice range. Let's make the range much longer so that several bullets are in flight at the same time. The three animations below show respectively the stationary gun, the gun moving toward the target, and the gun moving away from the target. "T" is the target, "G" is the gun, and the black dots are the bullets.

Stream of bullets from a stationary gun

Stream of bullets from a gun moving toward the target

Stream of bullets from a gun moving away from the target

If the shooter runs toward the target, he is firing the second bullet after having chased the first one. So the spacing between the two bullets is less than in the case of a stationary shooter. Comparing the videos, we can see that the bullets in flight are compressed closer together when the gun moves toward the target and are spread farther apart when the gun moves away.

What do these bullets have to do with sound?

Whenever vocal chords, guitar strings, or clarinet reeds vibrate, they launch waves of alternating bands of compression and expansion of the air, as shown in this animation:

WIKIFISICA2020, CC BY-SA 4.0 <https://creativecommons.org/licenses/by-sa/4.0>, via Wikimedia Commons

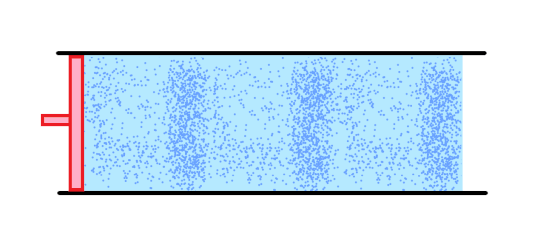
These bands of air compression travel through the air at the speed of sound, which at sea level is about 750 mph. The higher the frequency of vibration, the shorter the wavelength (the distance between successive bands).  The human ear translates the frequency of a sound wave into a perceived pitch, so the higher the frequency, the higher the pitch that will be heard.

Suppose that the source of the sound is getting closer to the listener. As in the case of the bullets, the bands of air compression get bunched closer together and reach the listener more often than they were created by the source. So, the frequency heard by the listener is elevated. If the source of the sound is getting farther away from the listener, the bands of air compression are stretched farther apart and the frequency heard by the listener is lowered. The animation at the top of this post shows this effect for a source of sound, such as a car horn, emitting sound waves in every direction. You can see that the wavelength is shortened ahead of the sound source and lengthened behind it. A stationary listener will hear a change of pitch from high to low as the horn passes by.

Running a red light legally, almost

I have a ludicrously fast sports car, and get pulled over by a police officer, who tells me that I ran a red light. Fortunately, I have a camera on my dashboard to prove the officer wrong, I show him the picture that it captured.

Officer, this light is green

Unfortunately, the officer's partner has a radar gun and she measured my speed at 193 million mph. That's almost 29% of the speed of light.

Fortunately, this did not happen to me. But the Doppler effect in the story is not fiction. Light consists of waves of electric and magnetic fields. Whenever an observer and a light source are moving closer together (due to the motion of either) the observer measures a shorter wavelength and a higher frequency than someone riding along with the light source. Whenever an observer and a light source are moving farther apart, the observer measures a longer wavelength and a lower frequency. For visible light, the human eye translates the frequency of a light wave into a perceived color. If the frequency change is large enough, as in my story, a person will see a change in color..

The Doppler effect is useful

The radar cop in the story is exploiting the Doppler effect. My car reflects the waves from her gun and becomes a source moving toward her. Weather radar uses the Doppler effect to measure wind speeds. Medical imaging techniques exist to measure blood flow velocity based on the Doppler effect.

For astronomers, the Doppler effect is a cosmic speedometer. Stars are made mostly of hydrogen, which absorbs light at particular wavelengths; this set of sharply defined wavelengths is like a fingerprint of hydrogen. The light from a star is darkened at these wavelengths because the hydrogen surrounding the star absorbs some of the light. When a star is getting closer or more distant from us, those wavelengths are shifted by the Doppler effect. This enables astronomers to deduce the velocity of a star relative to Earth along the line of sight.